written by @aw on 2017-1-5

reference: https://en.wikipedia.org/wiki/Direct-quadrature-zero_transformation

为什么要进行变换

我们要控制电机，就要控制电机的三相输入 $[a, b, c]$, 但是我们的数学理论，三唯向量对应的坐标系是一个直角坐标系 ${A, B, C}$. 而实际情况是我们的电机三个向量是在一个平面上，并且随着电机转动。
为了更好的进行数学计算，我们要把我们计算用的坐标系跟实际电机的坐标系统对应起来，这里就需要用到了坐标变换。这样我们在新的坐标系统内对三相的控制就能够真正的反应为电机的转动。

CLARK 变换

这个从三维直角坐标系变换到一个平面的过程我们称之为CLARK变换。
我们知道在电机内，三相的夹角为120度。想象一下，怎么把三维直接坐标系的三个轴映射到一个平面上，并且三轴在这个平面上的投影之间的夹角还正好为120度。
在直角坐标系内，有点 $(1, 1, 1)$，那么从原点到这个点的向量为 $[1, 1, 1]$，那么如果有一个平面垂直于向量 $[1,1,1]$ ，那么这个平面就是我们的电机平面，我们可以得到三轴在此平面上的投影之间的夹角正好是120度。

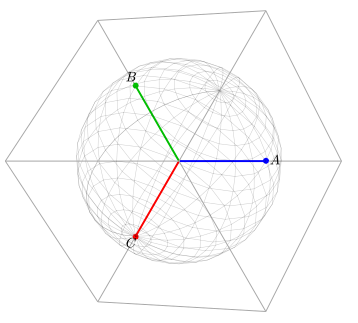
这个过程我们写成公式就是CLARK变换的公式，我们知道变换就是矩阵乘法。已知向量$[Va, Vb, Vc]$, 转换到电机平面对应为 $[X, Y, Z]$，其中Z轴对应的是原三维直角坐标系的原点。
变换过程，依靠旋转来进行。

旋转A轴 45度，这样$C$轴到了$C’$, $C’$ 的延长线到了立方体的边缘的中点位置。同理，$B$ 轴也被转到了 $Y$, 其延长线也到了立方体的边缘中点。

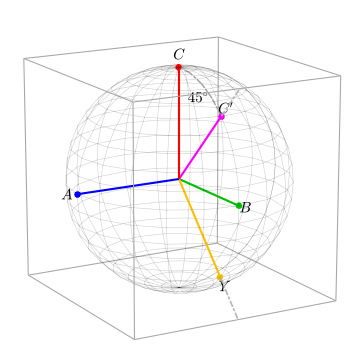
用数学式来表达就是：

旋转$Y$ 轴，使得 $C’$ 转到立方体的左上角，这个转动角度为35.26度。

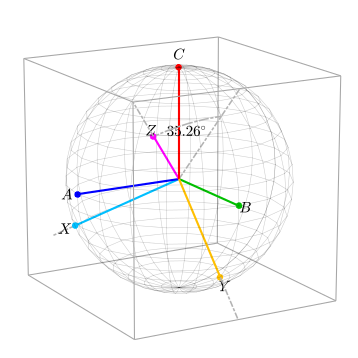
用数学式来表达就是

$\theta$， 35.26度是怎么求出来的？从圆心到立方体的边缘的中点的线段长 $\sqrt{2}$, 而球心到左上角的点构成的线段为 $\sqrt{3}$, 而另外一条边长为1。想象一下一个三角形三边分别为 $\sqrt{2}, \sqrt{3}, \sqrt{1}$, 这是一个直角三角形，因此 $\theta$ 很容易计算出来，

$\cos\theta = \sqrt{2/3}$, 所以 $\theta = 35.26^{。}$

最终，我们得到了新的坐标系 $X, Y, Z$, 我们可以看到我们都是在这个球上做的旋转。所有的向量的幅度都没有改变，保持了功率守恒。我们的马达平面就是图中的6边型所在的平面。可以看到Z轴垂直于这个平面，X, Y在这个平面上。

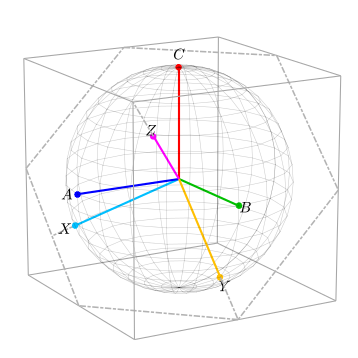
但是，注意一点，X, Y 的幅度(1)比A, B在此平面上的投影($\sqrt{2/3}$)要大。

整个变换公式为：

或者

为了计算方便，我们想办法让X,Y,Z轴跟A,B,C的投影一样大。如果把球压缩一下，X,Y,Z轴压缩到跟A,B,C的投影一样大，要压缩多少？$\sqrt{2/3}$
这样我们就得到了新公式

PARK 变换

我们推到出了CLARK变换，把三相电机的向量映射到了一个平面中。那这个X,Y 坐标系会跟着电机一块旋转，我们定义一个新的坐标系，还是在同一个平面内，有一个不转的坐标系D,Q,O。我们所有的计算在这个不变的坐标系内进行。这样坐标系D,Q,O和坐标系X,Y,Z就是一个旋转关系，绕Z轴或O轴旋转。

用公式表达就是X,Y,向量，乘以一个旋转矩阵。

这里的旋转角 $\theta$ 就是电机的转动角度。

综合

CLARK变换+PARK变换公式

如何通过控制VSI的6个开关来得到三相交流电

VSI

我们知道要把直流电变成交流电就需要Inverter, 如果供电电压是恒定的，我们需要VSI，如果供电电流是恒定的，我们需要CSI。

VSI，外部有一个恒压直流电源供电，通过控制6个开关（实际上只需要控制3个）来模拟三相交流电。

SVPWM控制开关

分为三个步骤，

计算Vd, Vq, 和角度 $\alpha$
计算时间 $T_{1}, T_{2}, T_{0}$
开关控制

计算Vd, Vq和角度 $\alpha$

如果我们已知相电压 $Va, Vb, Vc$, 那么我们根据CLARK变换公式，我们可以得到合成矢量为

$\begin{bmatrix} \ V_{d} \\ V_{q} \end{bmatrix} = \ \frac{2}{3} \ \begin{bmatrix} \ 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \ \begin{bmatrix} V_{an} \\ V_{bn} \\ V_{cn} \end{bmatrix}$ $\|V_{ref}\| = \sqrt{V_{d}^{2} + V_{q}^{2}}$ $\alpha = \tan^{-1}\left(\frac{V_{q}}{V_{d}}\right) = \omega t = 2\pi ft$

这里 $\omega$ 就是转动角速度

计算时间 $T_{1}, T_{2}, T_{0}$

只分析在第一个区间内的情况，其他的7个区间用同样的方法推导。

我们通过做功的角度来看，假如PWM的周期为 $T_{z}$。那么$V_{ref}$ 在时间 $T_{z}$ 内的做功可以分解为 $V_{1}$ 在 $T_{1}$ 内做的功和 $V_{2}$ 在 $T_{2}$ 做功之和。当然，$T_{z}$ 要足够小，能够匹配角速度的，也就是要求在 $T_{z}$ 时间内，电机转动的角度可以忽略不计。

实际上在很短的时间内，磁场的变化等于电压与时间的积 $\Delta \psi_{ref} = u_{ref} \dot \ \Delta t$

$V_{ref} T_{z} = V_{1} T_{1} + V_{2} T_{2}$

根据几何知识，我们可以计算出 $T_{1}, T_{2}$ 和 $T_{z}$ 的比例关系，

$T_{1} = T_{z} a \frac{\sin(\pi/3 - \alpha)}{\sin(\pi/3)}$ $T_{2} = T_{2} a \frac{\alpha}{\sin(\pi/3)}$ $T_{0} = T_{z} - T_{1} - T_{2}$

其中，$T_{z} = \frac{1}{f}, a = \frac{|V_{ref}|}{\frac{2}{3}Vdc}$

控制开关

Sector 1中

我们知道只有V1, V2两个向量起作用，而控制这两个向量的是开关组合分别是$(1, 0, 0)$ 和 $(1, 1 0)$, 为了防止谐波的产生，我们尽量少的减少开关的通断频率。因此，我们在设计我们的PWM波形时需要用对称的方式。

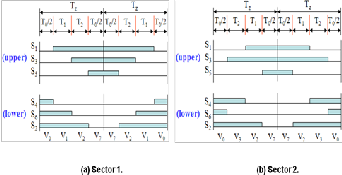
当转到其他的扇区的时候，用同样的思想去产生PWM来控制相应的开关，保持波形对称。

电机

参考资料