相机模型

最简单的相机模型就是利用小孔成像的原理来设计的。在物体(object)和胶片中间放一个遮挡(barrier)，这个遮挡上留一个小孔(pinhole, aperture)，这样我们再胶片上就能得到一个物体的倒影。

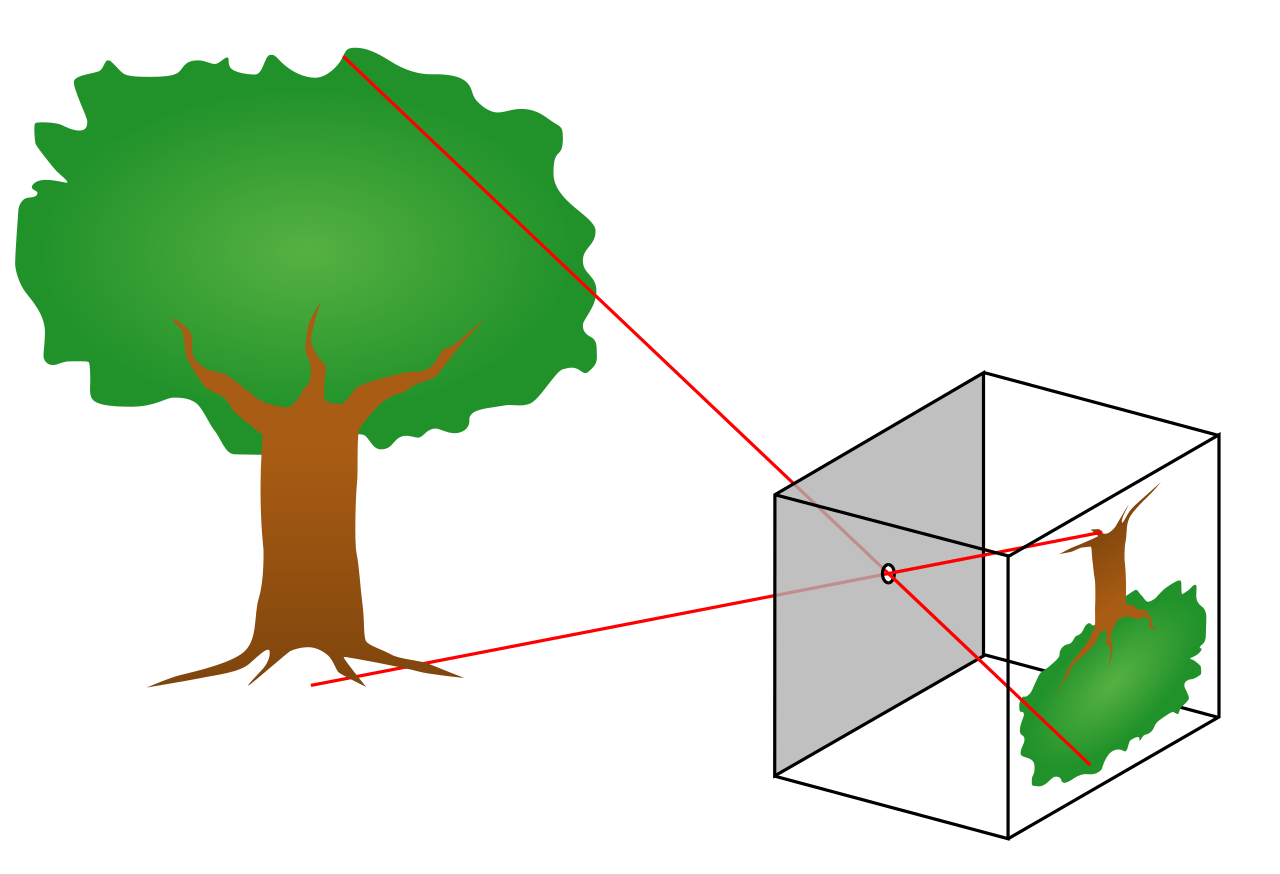
相机是一种把3D转换成2D的机器。

这个过程我们称之为投射 projection.

投射

经过投射后，景深信息丢失了，角度信息丢失了。直线信息保留了下来。
现实世界中的两条平行线变成了两条交叉线，交点为消失点Vanishing point.

针孔相机 pinhole camera

假设一个点P,坐标为 $(x, y, z)$，这个点投射到照片上的点为P’,坐标为 $(x’, y’)$. P和P’的关系满足下边的公式, f为焦距。

$x' = f\frac{x}{z} \\\\ y' = f\frac{y}{z}$

这个孔开多大合适呢？实际情况这个孔的大小跟光的波长有关系，不能大也不能太小。太大太小都会造成成像模糊。太小了会造成

光少
衍射

透镜相机 lens camera

对于透镜相机，拍摄物体时需要一个特殊的距离，我们称为”in forcus”，不在这个特殊距离的物体的点不会再胶片上聚焦，这样就形成了一个弥散圆 circle of confusion.

光学几何原理

当光通过一个介质 $n_{1}$ 进入另外一种介质 $n_{2}$ 的时候，在介质的表面会发生折射和反射，有3个角度，入射角 $\alpha_{1}$, 反射角 $\alpha_{2}$, 折射角 $\alpha_{3}$, 注意入射角和反射角相同。满足如下关系

$alpha_{1} = alpha_{2} \\\\ n1\sin\alpha_{1} = n2\sin\alpha_{3}$

透镜的问题

由于不同波长的光折射角不同，导致不同的光线的焦点不在同一点上。由于这个问题我们在拍到的照片的边缘会看到红光或者绿光。
Spherical aberration
Radial distortion, 这个我们会看到我们拍的照片是扭曲的，不是标准的四边形，有凹的，有凸的。像我们看到的鱼眼lens，就属于凸的情况。

Perspective matrix:

$\begin{bmatrix} \ f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \ \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} = \ \begin{bmatrix} fx \\ fy \\ z \\ \end{bmatrix} = \ \begin{bmatrix} \frac{fx}{z} \\ \frac{fy}{z} \\ 1 \\ \end{bmatrix} = K \ \begin{bmatrix} I & 0 \\ \end{bmatrix} \ P$ $K = \ \begin{bmatrix} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$

其中，f 为焦距, $(x, y, z)$为物体的空间坐标。这个公式表达了空间物体到照片坐标的转换公式。

当光轴中心点不在 $(0, 0)$时，如果光轴中心点在 $(u_{0}, v_{0})$,

$P' = K \ \begin{bmatrix} I & 0 \\ \end{bmatrix} \ P \implies w \ \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \ \begin{bmatrix} f & 0 & u_{0} & 0 \\ 0 & f & v_{0} & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \ \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}$

当像素不是矩形，而是长方形时

$P' = K \ \begin{bmatrix} I & 0 \\ \end{bmatrix} \ P \implies w \ \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \ \begin{bmatrix} \alpha & 0 & u_{0} & 0 \\ 0 & \beta & v_{0} & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \ \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}$

有倾斜时

$P' = K \ \begin{bmatrix} I & 0 \\ \end{bmatrix} \ P \implies w \ \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \ \begin{bmatrix} \alpha & s & u_{0} & 0 \\ 0 & \beta & v_{0} & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \ \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}$

Camera不在原点，而在 $(t_{x}, t_{y}, t_{z})$ 点时

$P' = K \ \begin{bmatrix} I & \vec{t} \\ \end{bmatrix} \ P \implies w \ \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \ \begin{bmatrix} \alpha & s & u_{0} & 0 \\ 0 & \beta & v_{0} & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \ \begin{bmatrix} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ \end{bmatrix} \ \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}$

camera 有旋转时 $P' = K \ \begin{bmatrix} R & \vec{t} \\ \end{bmatrix} \ P \implies w \ \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \ \begin{bmatrix} \alpha & s & u_{0} & 0 \\ 0 & \beta & v_{0} & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \ \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_{x} \\ r_{21} & r_{22} & r_{23} & t_{y} \\ r_{31} & r_{32} & r_{33} & t_{z} \\ \end{bmatrix} \ \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}$

Orthographic projection

就是被拍物体离COP 无限远，这意思就跟我们晚上看月亮，我们走感觉月亮的位置也不变其实是一个道理。

$w \ \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \ \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}$

weak perspective

物体的维度跟距离相比非常小

$w \ \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \ \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 0 & s \\ \end{bmatrix} \ \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}$

Field of view

也称为Zoom, 这个跟焦距有关。焦距越大，zoom越大，field of view 越小

立体视觉

照片中的什么信息可以被用于重建3D信号呢？

Shading
Texture
Focus
Motion
Others, such as highlights, shadows, silhouettes, inter-reflections, symmetry, light polarization …

Depth from convergence

假设双目的距离是c, 我们离目标点的距离为d, 光线从物体进入我们双眼形成的角度为$\alpha$, 那么这3个参数就构成了一个公式,

$d = \frac{c}{2\tan\left(\frac{\alpha}{2}\right)}$

对极几何 epipolar geometry

其中，$XO_{L}O_{R}$ 为对极面 epipolar plane, $O_{L}O_{R}$为基准线baseline，$X_{L}e_{L}$和$X_{R}e_{R}$为对极线epipolar lines, $e_{L}$, $e_{R}$ 为对极心 epipoles.

左边图像中重合的点$X$, $X_{1}$, $X_{2}$, $X_{3}$在右边图像上的对应点必然在对极线$X_{R}e_{R}$上，反之亦然。

极线约束 epipolar constrain

对于左边的相机L,

$X_{L} = M \ X = \ \begin{bmatrix} \ u \\ v \\ 1 \end{bmatrix} \\\\ M = K \ \begin{bmatrix} \ I & 0 \\ \end{bmatrix} \$

加入坐标系参考左边的相机坐标，那么对于右边的相机的坐标系就需要通过平移和旋转左边坐标系得到，假如变换矩阵为[R T],

对于右边的相机R

$X_{R} = M' \ X = \ \begin{bmatrix} \ u \\ v \\ 1 \end{bmatrix} \\\\ M' = K' \ \begin{bmatrix} \ R & T \\ \end{bmatrix} \$