线性代数复习
Vectors and Matrices
- 灰度图像用一个m x n的矩阵表达,因为每一个像素只有灰度信息(brightness)。
- 彩色图像用一个m x n x 3的矩阵表达,因为每一个像素包含RGB三色的亮度值。
內积(点积)Inner product(dot product)
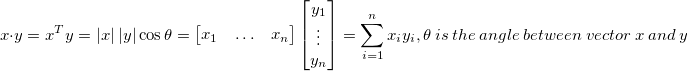
內积的几何意义:如果向量y是单位向量,那么dot(x, y)即向量x在向量y上的投影。
转置(transpose)
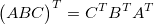
行列式(determinant)
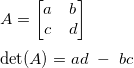
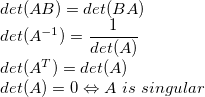
singular -> 奇异的, 也就是说奇异矩阵的行列式为0
行列式有一个几何意义:行向量组成的平行四边形的面积。
Trace
tr(A) = sum of diagonal elements
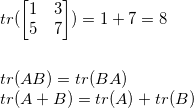
对称矩阵(Symmetric matrix)
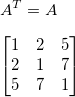
Screw-symmetric matrix
变换矩阵(Transformation Matrices)
矩阵乘法可以用来变换向量。这样的矩阵被称为变换矩阵, 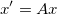
旋转(rotation)
一个向量p在原来的坐标系中,现在坐标系旋转了,那么p在新的坐标系中的坐标是什么? 可以用dot product很好的解决这个问题。
旋转矩阵(2D)
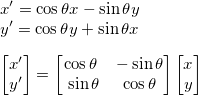
齐次坐标系(homogeneous system)
为什么引入齐次坐标系?总的来说,我们可以用矩阵乘以向量来表达各种线性变换,如缩放(scale),旋转(rotate),扭曲(skew). 但是有一点,我们无法往这些变换中加入常量。
因此我们引入了齐次坐标系,就是在原来的变换的矩阵,向量尾部加入常量 1,
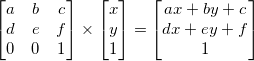
这样应用的话我们就往变换中加入了常量c,f. 这个变换过程就等效于原来的变化加上了一个常数向量,简洁一点就是变换+平移。
平移
那么变换矩阵就是单位矩阵,然后在跟平移的量构成一个齐次坐标系矩阵即可。
向量P在坐标系中平移t:
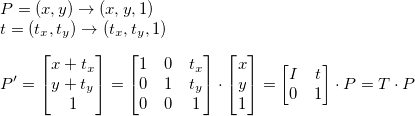
缩放
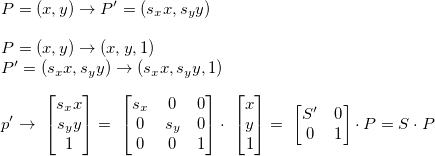
缩放平移
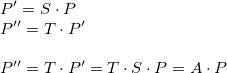
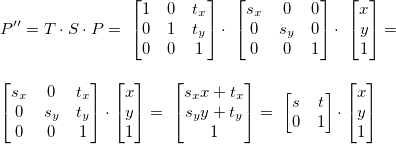
平移后缩放,跟缩放后平移得到的结果是不同的
平移后缩放,把之前的平移向量也同时缩放了。
旋转
- 旋转矩阵的转置是一个相反方向旋转的旋转矩阵。例如,一个旋转矩阵顺时针旋转了theta角,那么他的转置矩阵就是逆时针旋转了theta角
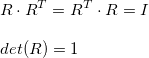
- 旋转矩阵的行向量之间是相互正交的,列向量也是一样
缩放旋转平移
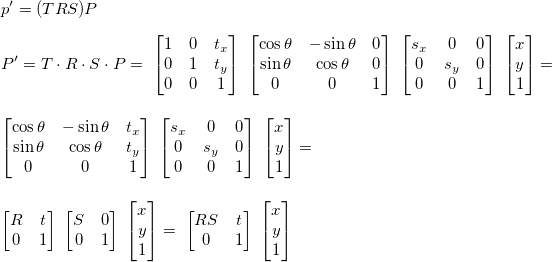
矩阵的逆
变换矩阵的逆是逆变换。
逆(Inverse)
如果一个矩阵存在逆矩阵,那么此矩阵是可逆的或者是非奇异矩阵。否则,就是奇异矩阵。
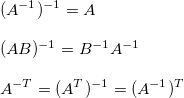
伪逆(Pseudoinverse)
对于大型的矩阵,用传统方法求他的逆的过程非常复杂,需要大量的计算。并且有些矩阵是不可逆的。在matlab中有一种用数值方法逼近求逆的方法,我们称之为伪逆。
如果有一个方程
Ax = B
传统的求此方程的方法为
inv(A) * A * x = inv(A) * B;
x = inv(A) * B;
这个计算量非常大,另外的方法
x = A \ B;
矩阵的秩(matrix rank)
线性独立(Linear independence)
假如有一组向量v1, …vn,
- 如果任何一个向量能用其他所有向量的线性组合来表示,那么这个向量是线性相关的。
- 如果任何一个向量都不能用其他向量的线性组合来表示,那么这个向量是线性独立的。
线性独立的向量组相互垂直。
矩阵的秩
表示矩阵中包含的向量中,线性独立的向量个数。
列向量的秩和行向量的秩是相等的
变换矩阵的秩告诉我们他把向量变换到几维空间。
例如,矩阵A的秩为1,那么变换 p’ = Ap 将所有点映射到一条直线上。
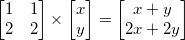
- 如果一个m x m的矩阵的秩为m,我们称之为满秩(full rank).
- 将一个m x 1向量映射为另一个m x 1向量
- 一定有逆矩阵
- 如果秩< m, 那么这个矩阵是奇异的(singular)
- 至少有一个向量是重叠的
- 不可逆
奇异值分解(SVD)
SVD可以把任何一个矩阵表达为3个矩阵相乘的形式,常用于寻找矩阵的特征值。
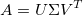
[U, S, V] = svd(A);
其中U, V是旋转矩阵,S是缩放矩阵。
如果 A是m x n 矩阵,那么U是m x m矩阵,S是m x n矩阵,V是n x n矩阵,这样运算的结果还是m x n矩阵 = A
SVD用于主分量分析(Principal Component Analysis, PCA),用在Machine Learning中可以用来减少特征值,从N维降低到N - M维,最终将到2维或者3维,就可以Plot出来了。
在机器视觉中,可以用来压缩图像。
svd的推导过程: http://www.ams.org/samplings/feature-column/fcarc-svd,
以后有时间再看推导过程吧,现在看着有点犯困。