从Linear regression中学习的gradient decent方法仍然可以应用到logistic regression.
分类(logistic regression)
之所以这里分类翻译成logistic regression是由于历史原因,究其原因是因为在分类方法中用到的sigmoid函数, 因为simgoid函数有一个别名, logistic函数。
分类问题,最简单的形式就是一堆数据,那些是这一类的,那些不是。在数学上简单描述一下可以认为
1. 是本类的:输出为1
2. 非本类的:输出为0
这种描述有个专门的术语叫 Binary classification,与之对应的是Multiple classification. 顾名思义,就是输出可以有多种,也就是可以把数据分成好多类,不单单是两类了。
Binary classification
他的描述可以用数学方式表述为
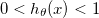
也就是说如果对这类问题设计算法,我们期望我们的系统输出结果在(0, 1)之间,然后配合相应的阈值,确定输出属于本类,或不属于本类。
数学上有一个经典的函数可以把输入映射到[0, 1]区间,sigmoid function, 它也被称为“logistic function”.
Sigmoid function:
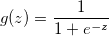
如果你有兴趣,可以通过以下的matlab代码看一下这个函数长什么样子
z = -1000 : 1000;
g = 1 / (1 + exp(-z));
plot(z, g);
有了sigmoid函数,我们可以得到我们的
hypothesis function
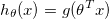
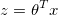
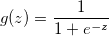
h(theta, x) = g(theta' * x)
z = theta' * x
g(z) = 1 / (1 + exp(-z))
根据sigmoid函数,可以得到以下的规律
- 当z >= 0时,g >= 0.5,可以认为输出为1
- 当z < 0时,g < 0.5, 可以认为输出为0
根据这个规律我们可以找到分类问题的边界,decision boundary
Decision boundary
根据sigmoid函数得到的规律,并且z = theta’ * x,可以得到
- 当theta’ * x >=0时,y = 1
- 当theta’ * x < 时,y = 0
这样就可以得到两类的边界,即
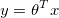
y = theta' * x
** 这里注意的是,这个边界不一定就是一个直线,虽然是用直线的表达式表述的,但是不要忘了x可以是polynomial. **