多项式拟合(Polynomial Regression)
多项式拟合实际上就是非线性拟合。如果数据无法用线性拟合或者用线性拟合后误差非常大,就需要考虑用非线性拟合。 现在比较一下线性拟合和多项式拟合的hypothesis function.
Linear regression:
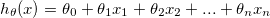
h = theta0 + theta1x1 + theta2x2 + ... + theta3x3
Polynomial regression:
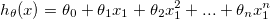
h = theta0 + theta1x1 + theta2x1^2 + ... + thetanx1^n
let x2 = x1^2, xn = x1^n, then,
h = theta0 + theta1x1 + theta2x2 + ... thetanxn # same as linear regression.
or,
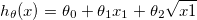
h = theta0 + theta1x1 + theta2sqrt(x1)
let x2 = sqrt(x1), then,
h = theta0 + theta1x1 + theta2x2 # same as linear regression.
特征归一化(Feature normalization)
特征归一化的目的是为了提高cost function的收敛速度。 theta值在小范围内收敛的速度明显比大范围快的多。基本思想就是把所有的特征值归一化到相同的范围内,一般情况下为(-0.5, 0.5)或 (-1, 1)。
达到特征归一化的方法有两种:
- Feature scaling
- Mean normalization.
Feature scaling
思路:某一特征值减去平均值后除以特征值范围。假设有一个特征xj, 均值用u表示,特征的最大值用xmax表示,最小值用xmin表示。那么用数学式表达feature scaling,即
xj = (xj - u) / (xmax - xmin)
Mean normalization
xj = (xj - u) / std, std为标准差
关于梯度下降法
我们可以通过画出关于迭代次数和cost function的曲线来调试算法是否合适。如果发现J不是单调递减的,那么就需要考虑调整学习率alpha.
如果alpha非常小,那么可以相信每次迭代,J都会下降,也就会最终得到正确的最小值。但是如果alpha选择的太小,要得到最小值,迭代次数就会非常多,就大大降低了算法的效率。 可以通过动态调整alpha的方法,即一旦发现J比之前的值大,将alpha变为原来的1/3, 此比例是prof Ng推荐的。